单调栈的使用

题目描述

84. 柱状图中最大的矩形
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。
示例:
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

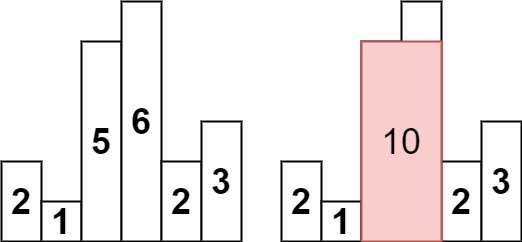
分析

暴力解法

• 从位置i出发, 向左向右延展, 构造高度为heights[i]的矩形
• 由于每次都要向左向右找到矩形边界(高度小于位置i的柱子), 时间复杂度O(N^2)
• 虽然会有几个点超时, 但这个思路是后续优化的出发点.

优化

因为最终的目的是寻找对应柱子height[i]右边首个严格小于height[i]的柱子height[r], 以及左边找到首个严格小于height[i]的柱子height[l].
维护一个单调递增栈(栈底->栈顶),那么每当遇到新加入的元素<栈顶便可以确定栈顶柱子右边界
而栈顶柱子左边界就是栈顶柱子下面的柱子(<栈顶柱子)
左右边界确定以后就可以进行面积计算与维护最大面积

题解

class Solution {
 public:
  int largestRectangleArea(vector<int>& heights) {
    heights.push_back(0);
    int result = 0, n = heights.size(), h, left;
    stack<int> st;
    for (int i = 0; i < n; ++i) {
      if (st.empty()) {
        st.push(i);
      } else {
        while (!st.empty() && heights[st.top()] >= heights[i]) {
          h = heights[st.top()];
          st.pop();
          left = st.empty() ? 0 : st.top() + 1;
          result = max(result, h * (i - left));
        }
        st.push(i);
      }
    }
    return result;
  }
};

类似的题目

85. 最大矩形: 给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

将列中连续的1转换为柱形, 然后根据情况采取暴力或者单调栈进行计算.